오차역전파법

앞 장에서는 weight parameter에 대한 loss function의 기울기를 수치 미분으로 구했다.

수치 미분은 단순하고 구현이 쉽지만 계산 시간이 오래 걸린다는 단점이 있다.

오차역전파법을 통해 weight parameter의 기울기를 효율적으로 계산한다.

계산 그래프

- 오차역전파법을 수식이 아닌 그래프를 통해 쉽게 이해해보기

계산 그래프란? - 계산 과정을 그래프로 나타낸 것

[계산 그래프에 익숙해지기]

Q1. A는 마트에서 1개에 100원인 사탕 2개를 샀다. 이때 지불 금액을 구하시오.(단, 소비세 10%가 부과된다.)
- Ver 1

Q1에 대한 계산 그래프 1

- Ver 2

Q1에 대한 계산 그래프 2 - '사과의 개수'와 '소비세'를 변수로 취급

Q2. A는 마트에서 사탕 2개와 젤리 3개를 샀다. 사탕은 1개에 100원, 젤리는 1개의 150원이다. 소비세가 10%일 때 지불 금액은?

Q2에 대한 계산 그래프

[계산 그래프를 이용한 문제 풀이 흐름]

1. 계산 그래프 구성

2. 왼쪽에서 오른쪽으로 진행(순전파)

 

역전파에 의한 미분 값의 전달(굵은 화살표)

 

연쇄법칙

위와 같은 국소적 미분은 역전파의 계산 순서이다. 이러한 방식은 미분값을 효율적으로 구할 수 있는데 왜 그런일이 가능한지 연쇄 법칙의 원리로 설명해본다.

연쇄법칙이란?

- 합성함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있다.

 

 

역전파

덧셈 노드의 역전파

ex. z = x+y -> 1을 곱하기만 할 뿐 입력된 값을 그대로 다음 노드로 보낸다.

곱셈 노드의 역전파

ex. z = xy -> '서로 바꾼 값'을 곱해서 다음 노드로 보낸다.

 

단순한 계층 구현하기

곱셈 계층

# 곱셈 계층 구현
class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None
    # 순전파 구현
    def forward(self, x, y):
        self.x = x
        self.y = y
        out = x*y
        return out
    # 역전파 구현
    def backward(self, dout):
        # x, y 바꾸기
        dx = dout * self.y
        dy = dout * self.x
        
        return dx, dy

# Q1 구현
candy = 100
candy_num = 2
tax = 1.1

# 계층들
mul_candy_layer = MulLayer()
mul_tax_layer = MulLayer()

candy_price = mul_candy_layer.forward(candy, candy_num)
price = mul_tax_layer.forward(candy_price, tax)

print(price)

output : 220

# 역전파
dprice = 1
dcandy_price, dtax = mul_tax_layer.backward(dprice)
dcandy, dcandy_num = mul_candy_layer.backward(dcandy_price)

print(dcandy, dcandy_num, dtax)

output : 2.2 110 200

 

덧셈 계층

# 덧셈 계층 구현
class MulLayer:
    # 덧셈 계층에는 초기화 필요 x
    def __init__(self):
        pass
    
    # 순전파 구현
    def forward(self, x, y):
        out = x+ y
        return out
    
    # 역전파 구현
    def backward(self, dout):
        # x, y 바꾸기
        dx = dout * 1
        dy = dout * 1
        
        return dx, dy

# Q2 구현

apple = 100
apple_num = 2
orange = 150
orange_num = 3
tax = 1.1

# layer
mul_apple_layer = MulLayer()
mul_orange_layer = MulLayer()
add_apple_orange_layer = AddLayer()
mul_tax_layer = MulLayer()

# forward
apple_price = mul_apple_layer.forward(apple, apple_num)  # (1)
orange_price = mul_orange_layer.forward(orange, orange_num)  # (2)
all_price = add_apple_orange_layer.forward(apple_price, orange_price)  # (3)
price = mul_tax_layer.forward(all_price, tax)  # (4)

# backward
dprice = 1
dall_price, dtax = mul_tax_layer.backward(dprice)  # (4)
dapple_price, dorange_price = add_apple_orange_layer.backward(dall_price)  # (3)
dorange, dorange_num = mul_orange_layer.backward(dorange_price)  # (2)
dapple, dapple_num = mul_apple_layer.backward(dapple_price)  # (1)

print("price:", int(price))
print("dApple:", dapple)
print("dApple_num:", int(dapple_num))
print("dOrange:", dorange)
print("dOrange_num:", int(dorange_num))
print("dTax:", dtax)

output : 715

output : 110 2.2 3.3 165 650

 

 

활성화 함수 계층 구현하기

ReLu 계층

class Relu:
    def __init__(self):
        self.mask = None
        
    def forward(self, x):
        self.mask = (x <= 0)
        out = x.copy()
        out[self.mask] = 0
        return out
    
    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        return dx

- mask는 True/False로 구성된 배열(입력인 x의 원소값이 0이하면 True, 그외는 False)

- True인 경우에는 0을 흘려보냄.

 

Sigmoid 계층

Sigmoid 함수

Sigmoid 계층의 계산 그래프(순전파)

Step 1. '/' 노드 미분 즉 y = 1/x를 미분 -> - y**2

Step 2. '+' 노드는 여과 없이 흘려보냄

Step 3. 'exp' 노드 -> - y**2*exp(-x)

Step 4. 'x'노드는 값을 서로 바꿔서 흘려 보냄 -> y**2*exp(-x)

 

간소화 Version

간소화 과정 증명

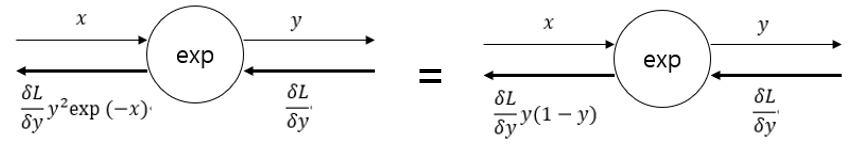
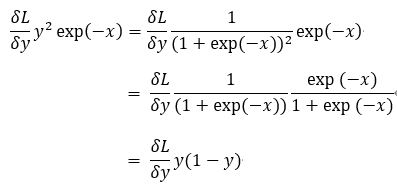
- Sigmoid 계층의 역전파는 순전파의 출력값(y)만으로 계산 가능

import numpy as np
class Sigmoid:
    def __init__(self):
        self.out = None
        
    def forward(self, x):
        out = 1 / (1+np.exp(-x))
        self.out = out
        return out
    
    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        return dx

 

Affine/Softmax 계층 구현하기

Affine 계층

Affine 계층 계산 그래프(변수가 행렬임)

Affine 계층의 역전파(입력 데이터 X 한개)

배치용 Affine 계층

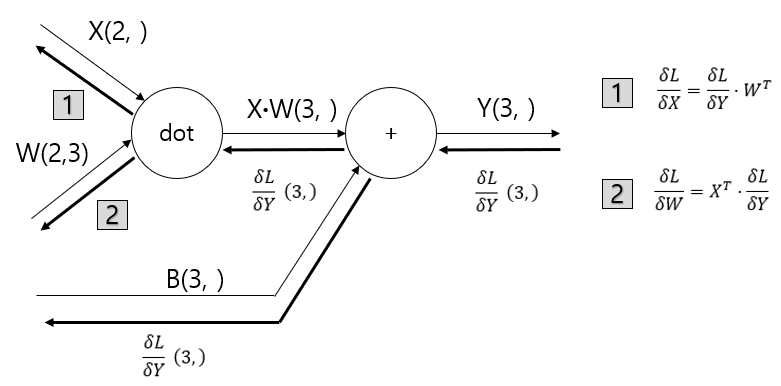
배치용 Affine 계층의 계산 그래프

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.dW = None
        self.db = None
        
    def forward(self, x):
        self.x = x
        out = np.dot(x, self.W) + self.b
        
        return out
    
    def backward(self, dout):
        dx = np.dot(dout, self.W.T)
        self.dw = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        
        return dx

 

Softmax 계층

- Softmax 함수는 입력 값을 정규화하여 출력한다.(출력의 합이 1이 되도록)

간소화한 Softmax-with-Loss 계층의 계산 그래프

- 역전파로 Softmax계층의 출력값과 정답 레이블의 차이(y-t)를 전달

class SoftmaxWithLoss:
    def __init__(self):
        self.loss = None #손실
        self.y = None # Softmax의 출력
        self.t = None # 정답 레이블
        
    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self,t)
        return self.loss
    
    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        dx = (self.y - self.t) / batch_size
        
        return dx

 

오차역전파법 구현하기

[정리]

step 1. 미니배치

- 훈련 데이터 중 일부를 무작위로 추출. 미니 배치의 loss function값을 줄이는 것이 목표

step 2. 기울기 산출(오차 역전파법이 적용되는 step)

- 미니배치의 loss function값을 줄이기 위해 각 weight parameter의 기울기를 구함. 기울기는 loss function값을 가장 작게하는 방향으로 제시

step 3. 매개변수 갱신

- weight parameter를 기울기 방향으로 조금 갱신

step 3. 반복

- 1~3 step을 반복

 

(코드 생략 - 다음 글에 upload)